
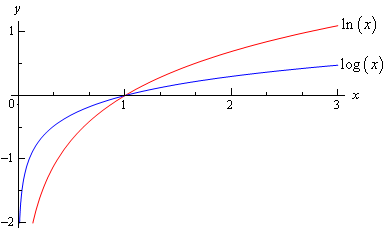
To the right of 1 on the x-axis, the function f continually increases, but increases more and more slowly as x heads towards infinity. Since any positive real number raised to the exponent zero is 1, the logarithm of 1 is zero. Thus, for any base b > 1 logarithms of numbers between 0 and 1 are negative numbers, the logarithm of 1 is 0, and logarithms of numbers greater than 1 are positive real numbers as seen in the image below.Ĭonsider the function f( x) = log b( x) where b is a real-number base greater than 1 of the logarithm. Multiplying a number by 10 appends a zero to the numeral (if it is an integer) and adds 1 to the base-10 logarithm, therefore log 10(430) is approximately 2.63347.īy a similar argument it can be established that b 0 = 1 for any base b > 1 and therefore that log b(1) = 0. For example, log 10(43) is approximately equal to 1.63347. Values for many other numbers can be worked out similarly using cube roots and so on, and values for all real numbers can then be defined using limits. We know from the study of exponents that, for example, is and this then supplies a value for. (The value of the logarithmic function is the number that appeared as an exponent in the other equation.) But what is the logarithm of a number such as 43, or 0.001?
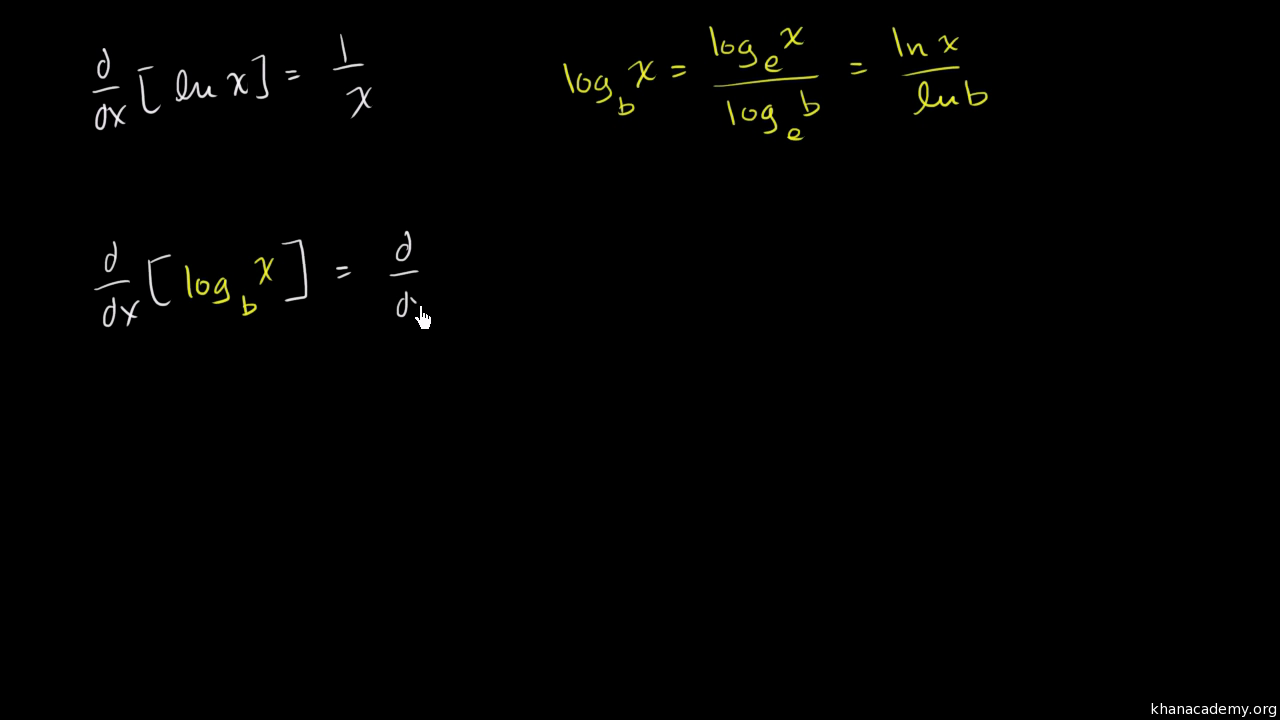
It's easy to find the base-10 logarithm of a number such as 1000, because 1000 = 10 3, therefore log 10(1000) = 3. Logarithms of intermediate and fractional valuesīecause we use a base-10 number system, it is often convenient to use 10 as the base of the logarithm. 7.2 After the advent of calculators and computers.7.1 Before the advent of calculators and computers.1 Logarithms of intermediate and fractional values.Let u = -4x + 1 and y = ln u, Use the chain rule to find the derivative of function f as follows.= / (1 - x) 2Įxample 4 Find the derivative of f(x) = ln (-4x + 1) Hence we use the quotient rule, f '(x) = / h(x) 2, to find the derivative of function f.į '(x) = / h(x) 2 Let g(x) = log 3 x and h(x) = 1 - x, function f is the quotient of functions g and h: f(x) = g(x) / h(x).Use the sum rule, f '(x) = g '(x) + h '(x), to find the derivative of function fĮxample 3 Find the derivative of f(x) = log 3 x / ( 1 - x ) Let g(x) = ln x and h(x) = 6x 2, function f is the sum of functions g and h: f(x) = g(x) + h(x).Note: if f(x) = ln x, then f '(x) = 1 / xĮxamples Example 1 Find the derivative of f(x) = log 3 xĮxample 2 Find the derivative of f(x) = ln x + 6x 2 The first derivative of f(x) = log b x is given by First Derivative of a Logarithmic Function to any Base


 0 kommentar(er)
0 kommentar(er)
